Codeforces: Round #705 (Div.2)
Codeforces
A. Anti-knapsack
You are given two integers $𝑛$ and $𝑘$. You are asked to choose maximum number of distinct integers from 1 to $𝑛$ so that there is no subset of chosen numbers with sum equal to $𝑘$.
A subset of a set is a set that can be obtained from initial one by removing some (possibly all or none) elements of it.
Input
The first line contains the number of test cases $𝑇$ $(1≤𝑇≤100)$.
Each of the next $𝑇$lines contains two integers $𝑛$ and $𝑘$ $(1≤𝑘≤𝑛≤1000)$ — the description of test cases.
Output
For each test case output two lines. In the first line output a single integer $𝑚$ — the number of chosen integers.
In the second line output $𝑚$ distinct integers from $1$ to $𝑛$ — the chosen numbers.
If there are multiple answers, print any. You can print the numbers in any order.
풀이
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
int n, k; cin >> n >> k;
cout << n - (k + 1) / 2 << "\n";
for (int i = k + 1; i <= n; i++) cout << i << " ";
for (int i = (k + 1) / 2; i < k; i++) cout << i << " ";
cout << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
return 0;
}
B. Planet Lapituletti
The time on the planet Lapituletti goes the same way it goes on Earth but a day lasts $ℎ$ hours and each hour lasts $𝑚$ minutes. The inhabitants of that planet use digital clocks similar to earth ones. Clocks display time in a format HH:MM (the number of hours in decimal is displayed first, then (after the colon) follows the number of minutes in decimal; the number of minutes and hours is written with leading zeros if needed to form a two-digit number). Hours are numbered from $0$ to $ℎ−1$ and minutes are numbered from $0$ to $𝑚−1$.
 That’s how the digits are displayed on the clock. Please note that digit $1$ is placed in the middle of its position.
That’s how the digits are displayed on the clock. Please note that digit $1$ is placed in the middle of its position.
A standard mirror is in use on the planet Lapituletti. Inhabitants often look at the reflection of the digital clocks in the mirror and feel happy when what you see on the reflected clocks is a valid time (that means that you see valid digits in the reflection and this time can be seen on the normal clocks at some moment of a day).
The image of the clocks in the mirror is reflected against a vertical axis.
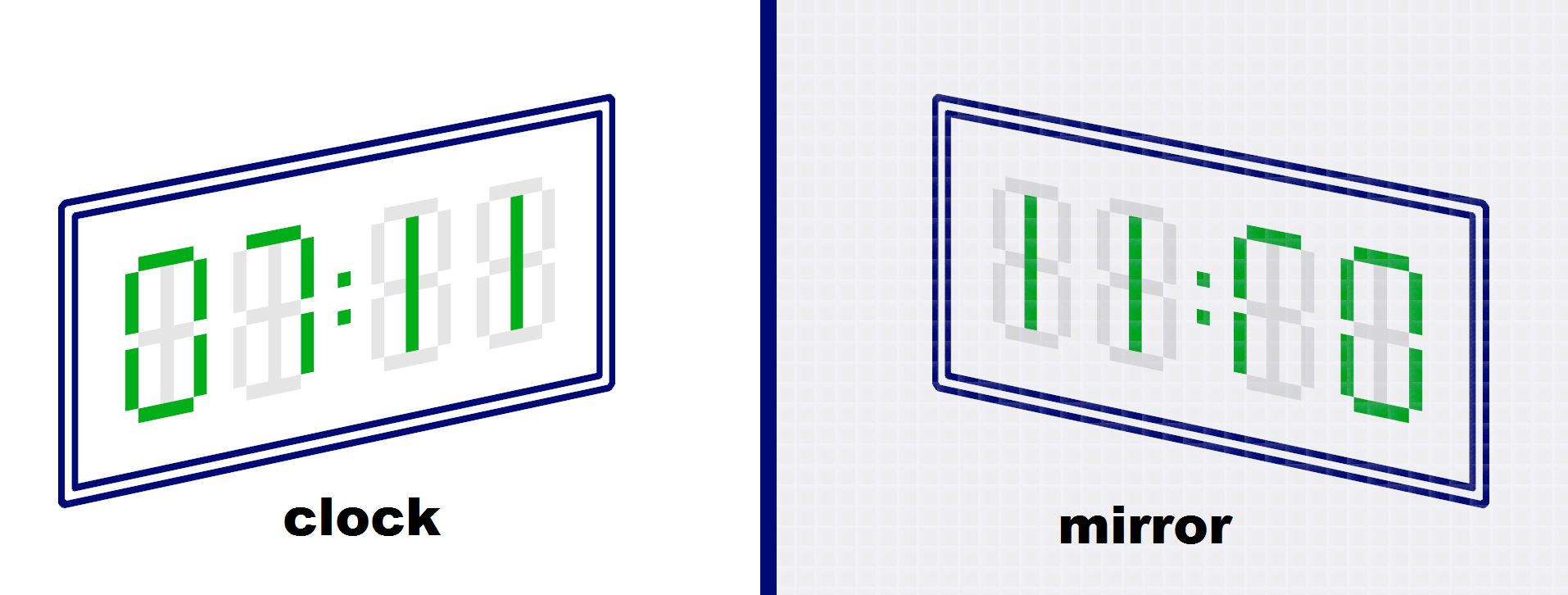 The reflection is not a valid time.
The reflection is not a valid time.
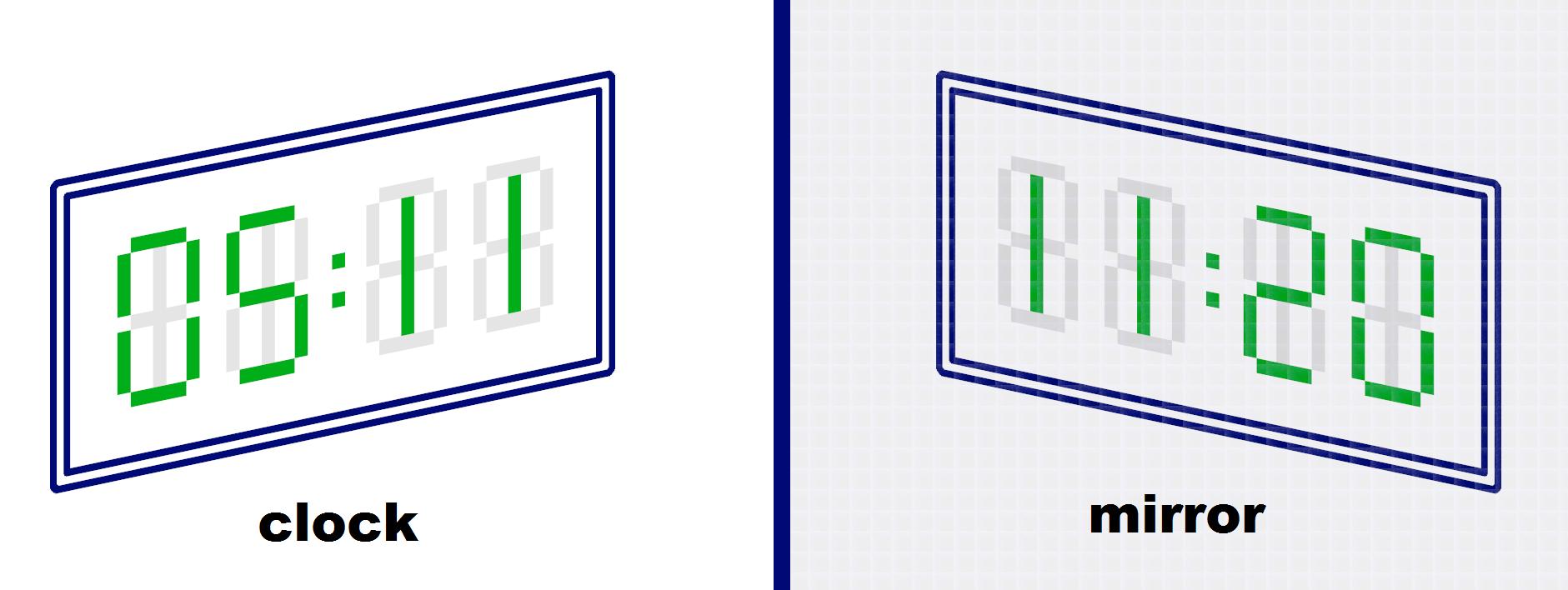 The reflection is a valid time with $ℎ=24$, $𝑚=60$. However, for example, if $ℎ=10$, $𝑚=60$, then the reflection is not a valid time.
The reflection is a valid time with $ℎ=24$, $𝑚=60$. However, for example, if $ℎ=10$, $𝑚=60$, then the reflection is not a valid time.
An inhabitant of the planet Lapituletti begins to look at a mirrored image of the clocks at some time moment $𝑠$ and wants to know the nearest future time moment (which can possibly happen on the next day), when the reflected clock time is valid.
It can be shown that with any $ℎ, 𝑚, 𝑠$ such a moment exists. If the reflected time is correct at the moment the inhabitant began to look at the clock, that moment is considered the nearest.
You are asked to solve the problem for several test cases.
Input
The first line contains a single integer $𝑇$ $(1≤𝑇≤100)$ — the number of test cases.
The next $2⋅𝑇$ lines contain the description of test cases. The description of each test case consists of two lines.
The first line of a test case contains two integers $ℎ, 𝑚$ $(1≤ℎ,𝑚≤100)$.
The second line contains the start time $𝑠$ in the described format HH:MM.
Output
For each test case output in a separate line the nearest moment in format HH:MM when the reflected time is correct.
풀이
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int pos[10] = {0, 1, 5, -1, -1, 2, -1, -1, 8, -1};
bool chk(int n) {
if(n == 0 || n == 1 || n == 2 || n == 5 || n == 8) return true;
return false;
}
void solve() {
// 0, 1, 2, 5, 8
int h, m; cin >> h >> m;
string s; cin >> s;
int h_1 = s[0] - '0', h_2 = s[1] - '0', m_1 = s[3] - '0', m_2 = s[4] - '0';
int start_h = 10 * h_1 + h_2;
int start_m = 10 * m_1 + m_2;
for (int i = start_h; i < h; i++) {
for (int j = (i == start_h ? start_m : 0); j < m; j++) {
if (i != start_h) { m_1 = 0; m_2 = 0; }
if (chk(h_1) && chk(h_2) && chk(m_1) && chk(m_2)) {
int rev_h = 10 * pos[m_2] + pos[m_1], rev_m = 10 * pos[h_2] + pos[h_1];
if (rev_h < h && rev_m < m) {
cout << h_1 << h_2 << ":" << m_1 << m_2 << "\n";
return;
}
}
if (m_2 < 9) m_2++;
else { m_1++; m_2 = 0; }
}
if (h_2 < 9) h_2++;
else { h_1++; h_2 = 0; }
}
cout << "00:00\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
return 0;
}
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int H, M;
int X[10] = {0, 1, 5, -1, -1, 2, -1, -1, 8, -1};
bool valid(int h, int m) {
if(X[m % 10] == -1 || X[m / 10] == -1) return false;
int th = X[m % 10] * 10 + X[m / 10];
if(X[h % 10] == -1 || X[h / 10] == -1) return false;
int tm = X[h % 10] * 10 + X[h / 10];
if(th >= H || tm >= M) return false;
return true;
}
int main() {
int tc; scanf("%d", &tc);
while(tc--) {
scanf("%d%d", &H, &M);
int h, m; scanf("%02d:%02d", &h, &m);
while(1) {
if(valid(h, m)) break;
m++;
if(m >= M) { m = 0; h++; }
if(h >= H) h -= H;
}
printf("%02d:%02d\n", h, m);
}
return 0;
}
C. K-beautiful Strings
You are given a string 𝑠 consisting of lowercase English letters and a number $𝑘$. Let’s call a string consisting of lowercase English letters beautiful if the number of occurrences of each letter in that string is divisible by $𝑘$. You are asked to find the lexicographically smallest beautiful string of length $𝑛$, which is lexicographically greater or equal to string $𝑠$. If such a string does not exist, output $−1$.
A string $𝑎$ is lexicographically smaller than a string $𝑏$ if and only if one of the following holds:
- $𝑎$ is a prefix of $𝑏$, but $𝑎≠𝑏$;
- in the first position where $𝑎$ and 𝑏 differ, the string $𝑎$ has a letter that appears earlier in the alphabet than the corresponding letter in $𝑏$.
Input
The first line contains a single integer $𝑇$ $(1≤𝑇≤10000)$ — the number of test cases.
The next $2⋅𝑇$ lines contain the description of test cases. The description of each test case consists of two lines.
The first line of the description contains two integers $𝑛$ and $𝑘$ $(1≤𝑘≤𝑛≤10^5)$ — the length of string $𝑠$ and number $𝑘$ respectively.
The second line contains string $𝑠$ consisting of lowercase English letters.
It is guaranteed that the sum of $𝑛$ over all test cases does not exceed $10^5$.
Output
For each test case output in a separate line lexicographically smallest beautiful string of length $𝑛$, which is greater or equal to string $𝑠$, or $−1$ if such a string does not exist.
풀이
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int N, K;
int cnt[30];
char A[101010];
int main() {
int tc; scanf("%d", &tc);
while(tc--) {
scanf("%d%d", &N, &K);
scanf("%s", A + 1);
if(N % K) { puts("-1"); continue; }
for(int i = 0; i < 26; i++) cnt[i] = 0;
for(int i = 1; i <= N; i++) cnt[A[i] - 'a']++;
bool ok = true;
for(int i = 0; i < 26; i++) if(cnt[i] % K) ok = false;
if(ok) { printf("%s\n", A + 1); continue; }
for(int i = N - 1; i >= 0; i--) {
char c = A[i + 1];
cnt[c - 'a']--;
ok = false;
for(int j = c + 1; j <= 'z'; j++) {
cnt[j - 'a']++;
int x = 0;
for(int k = 0; k < 26; k++) x += (K - cnt[k] % K) % K;
if(x > N - i - 1) { cnt[j - 'a']--; continue; }
A[i + 1] = j;
int lft = N - i - 1 - x;
int k = i + 2;
while(lft) { A[k] = 'a'; lft--; k++; }
int p = 'a';
for(; k <= N; k++) {
while(p <= 'z' && cnt[p - 'a'] % K == 0) p++;
if(p > 'z') break;
A[k] = p; cnt[p - 'a']++;
}
ok = true;
break;
}
if(ok) break;
}
printf("%s\n", A + 1);
}
return 0;
}
