Codeforces: Round #702 (Div.3)
Codeforces
A. Dense Array
For example, the arrays $[1,2,3,4,3]$, $[1,1,1]$ and $[5,10]$ are dense. And the arrays $[5,11]$, $[1,4,2]$, $[6,6,1]$ are not dense.
You are given an array $a$ of $n$ integers. What is the minimum number of numbers you need to add to an array to make it dense? You can insert numbers anywhere in the array. If the array is already dense, no numbers need to be added.
For example, if $a=[4,2,10,1]$, then the answer is $5$, and the array itself after inserting elements into it may look like this: $a=[4,2,\mathbf{\underline{3}},\mathbf{\underline{5}},10,\mathbf{\underline{6}},\mathbf{\underline{4}},\mathbf{\underline{2}},1]$ (there are other ways to build such $a$).
Input
The first line contains one integer $t$ $(1≤t≤1000)$. Then $t$ test cases follow.
The first line of each test case contains one integer $n$ $(2≤n≤50)$ — the length of the array $a$.
The next line contains $n$ integers $a_1,a_2,…,a_n$ $(1≤a_i≤50)$.
Output
For each test case, output one integer — the minimum number of numbers that must be added to the array to make it dense.
풀이
// TODO
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
int n; cin >> n;
vector<int> v(n);
for (int i = 0; i < n; i++) {
cin >> v[i];
}
int cnt = 0;
for (int i = 0; i < n - 1; i++) {
int mx = max(v[i], v[i + 1]);
int mn = min(v[i], v[i + 1]);
while ( (mx + mn - 1) / mn > 2) {
mn = mn * 2;
cnt++;
}
}
cout << cnt << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
return 0;
}
B. Balanced Remainders
You are given a number $n$ (divisible by $3$) and an array $a[1…n]$. In one move, you can increase any of the array elements by one. Formally, you choose the index $i$ $(1≤i≤n)$ and replace 𝑎𝑖 with $a_i+1$. You can choose the same index $i$ multiple times for different moves.
Let’s denote by $c_0$, $c_1$ and $c_2$ the number of numbers from the array $a$ that have remainders $0$, $1$ and $2$ when divided by the number $3$, respectively. Let’s say that the array $a$ has balanced remainders if $c_0$, $c_1$ and $c_2$ are equal.
For example, if $n=6$ and $a=[0,2,5,5,4,8]$, then the following sequence of moves is possible:
- initially $c_0=1$, $c_1=1$ and $c_2=4$, these values are not equal to each other. Let’s increase $a_3$, now the array $a=[0,2,6,5,4,8]$;
- $c_0=2$, $c_1=1$ and $c_2=3$, these values are not equal. Let’s increase $a_6$, now the array $a=[0,2,6,5,4,9]$;
- $c_0=3$, $c_1=1$ and $c_2=2$, these values are not equal. Let’s increase $a_1$, now the array $a=[1,2,6,5,4,9]$;
- $c_0=2$, $c_1=2$ and $c_2=2$, these values are equal to each other, which means that the array $a$ has balanced remainders.
Find the minimum number of moves needed to make the array $a$ have balanced remainders.
Input
The first line contains one integer $t$ $(1≤t≤10^4)$. Then $t$ test cases follow.
The first line of each test case contains one integer $n$ $(3≤n≤3⋅10^4)$ — the length of the array $a$. It is guaranteed that the number $n$ is divisible by $3$.
The next line contains $n$ integers $a_1,a_2,…,a_n$ $(0≤a_i≤100)$.
It is guaranteed that the sum of $n$ over all test cases does not exceed $150000$.
Output
For each test case, output one integer — the minimum number of moves that must be made for the $a$ array to make it have balanced remainders.
풀이
// TODO
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
int n; cin >> n;
vector<int> v(3);
for (int i = 0; i < n; i++) {
int k; cin >> k;
v[k % 3]++;
}
int c = n / 3;
int cnt = 0;
while (!(v[0] == c && v[1] == c && v[2] == c)) {
for (int i = 0; i < 3; i++) {
if (v[i] >= c && v[(i + 1) % 3] < c) {
cnt += c - v[(i + 1) % 3];
v[i] -= c - v[(i + 1) % 3];
v[(i + 1) % 3] = c;
}
}
}
cout << cnt << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
return 0;
}
C. Sum of Cubes
You are given a positive integer $x$. Check whether the number $x$ is representable as the sum of the cubes of two positive integers.
Formally, you need to check if there are two integers $a$ and $b$ $(1≤a,b)$ such that $a^3+b^3=x$.
For example, if $x=35$, then the numbers $a=2$ and $b=3$ are suitable $(2^3+3^3=8+27=35)$. If $x=4$, then no pair of numbers $a$ and $b$ is suitable.
Input
The first line contains one integer $t$ $(1≤t≤100)$ — the number of test cases. Then $t$ test cases follow.
Each test case contains one integer $x$ $(1≤x≤10^{12})$.
Please note, that the input for some test cases won’t fit into $32$-bit integer type, so you should use at least $64$-bit integer type in your programming language.
Output
For each test case, output on a separate line:
- “YES” if $x$ is representable as the sum of the cubes of two positive integers.
- “NO” otherwise.
You can output “YES” and “NO” in any case (for example, the strings yEs, yes, Yes and YES will be recognized as positive).
풀이
// TODO
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
ll x; cin >> x;
ll l = 1, r = 10000;
bool pos = false;
while (l <= r) {
if (l * l * l + r * r * r == x) {
pos = true;
break;
}
else if (l * l * l + r * r * r < x) l++;
else r--;
}
cout << (pos ? "YES" : "NO") << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
return 0;
}
D. Permutation Transformation
A permutation — is a sequence of length $n$ integers from 1 to $n$, in which all the numbers occur exactly once. For example, $[1]$, $[3,5,2,1,4]$, $[1,3,2]$ — permutations, and $[2,3,2]$, $[4,3,1]$, $[0]$ — no.
Polycarp was recently gifted a permutation $a[1…n]$ of length $n$. Polycarp likes trees more than permutations, so he wants to transform permutation $a$ into a rooted binary tree. He transforms an array of different integers into a tree as follows:
- the maximum element of the array becomes the root of the tree;
- all elements to the left of the maximum — form a left subtree (which is built according to the same rules but applied to the left part of the array), but if there are no elements to the left of the maximum, then the root has no left child;
- all elements to the right of the maximum — form a right subtree (which is built according to the same rules but applied to the right side of the array), but if there are no elements to the right of the maximum, then the root has no right child.
For example, if he builds a tree by permutation $a=[3,5,2,1,4]$, then the root will be the element $a_2=5$, and the left subtree will be the tree that will be built for the subarray $a[1…1]=[3]$, and the right one — for the subarray $a[3…5]=[2,1,4]$. As a result, the following tree will be built:
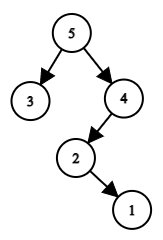 The tree corresponding to the permutation $a=[3,5,2,1,4]$.
The tree corresponding to the permutation $a=[3,5,2,1,4]$.
Another example: let the permutation be $a=[1,3,2,7,5,6,4]$. In this case, the tree looks like this:
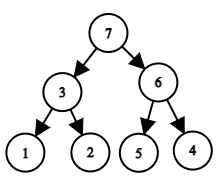 The tree corresponding to the permutation $a=[1,3,2,7,5,6,4]$.
The tree corresponding to the permutation $a=[1,3,2,7,5,6,4]$.
Let us denote by $d_v$ the depth of the vertex $a_v$, that is, the number of edges on the path from the root to the vertex numbered $a_v$. Note that the root depth is zero. Given the permutation $a$, for each vertex, find the value of $d_v$.
Input
The first line contains one integer $𝑡$ $(1≤𝑡≤100)$ — the number of test cases. Then 𝑡 test cases follow.
The first line of each test case contains an integer $𝑛$ $(1≤𝑛≤100)$ — the length of the permutation.
This is followed by $𝑛$ numbers $𝑎_1,𝑎_2,…,𝑎_𝑛$ — permutation $𝑎$.
Output
For each test case, output $𝑛$ values — $𝑑_1,𝑑_2,…,𝑑_𝑛$.
풀이
Divide & Conquer
코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[100];
int d[100];
void dfs(int start, int end, int depth) {
if (start > end) return;
int mx = 0, idx = 0;
for (int i = start; i <= end; i++) {
if (mx < a[i]) mx = a[i], idx = i;
}
d[idx] = depth;
dfs(start, idx - 1, depth + 1);
dfs(idx + 1, end, depth + 1);
}
void solve() {
int n; cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
dfs(0, n - 1, 0);
for (int i = 0; i < n; i++) {
cout << d[i] << " \n" [i == n - 1];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
return 0;
}
